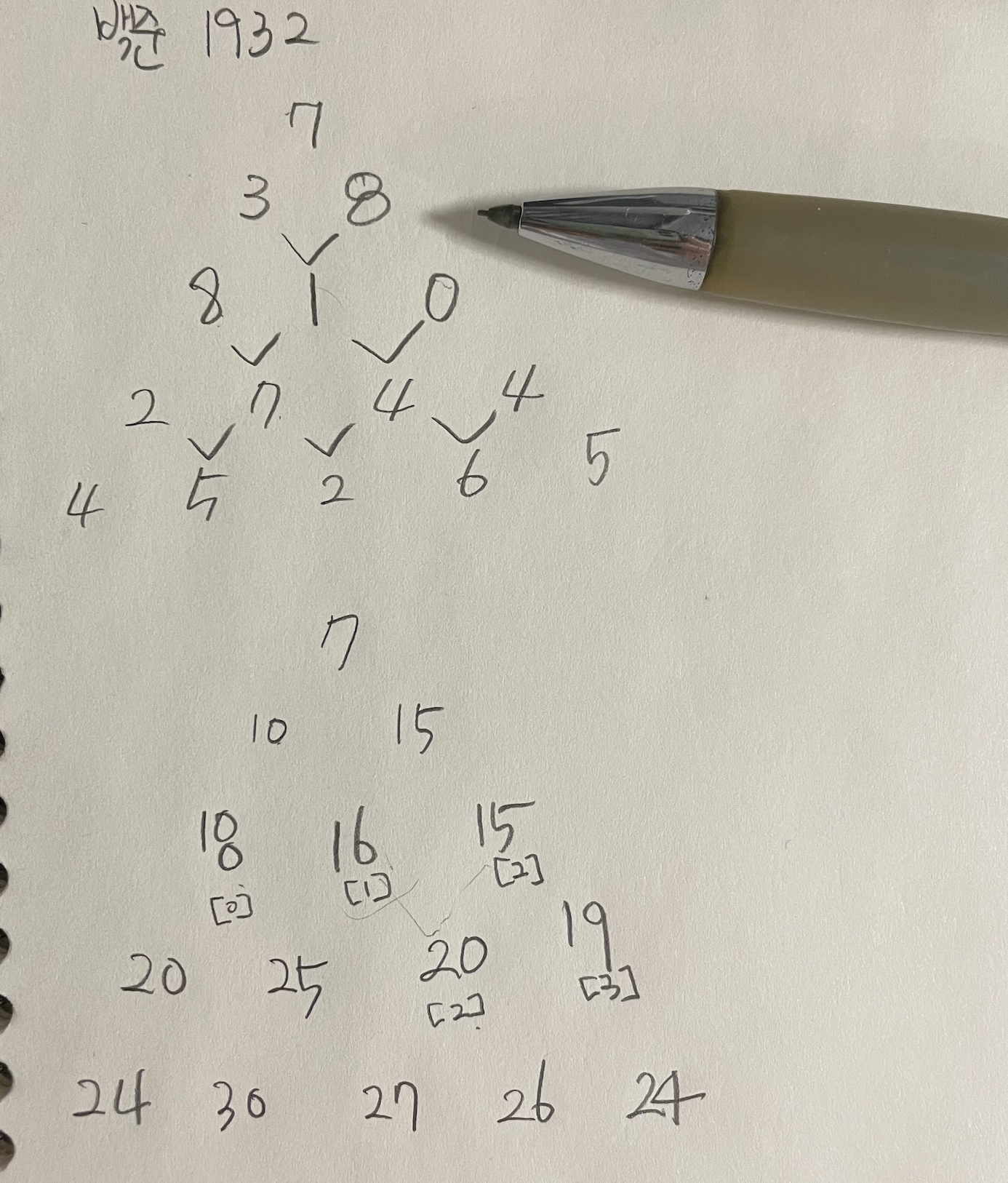lgvv98

BOJ 1932 정수 삼각형 ✅ dp를 이용한 문제였는데, 스스로 점화식을 찾아서 풀었다~! 처음으로 점화식을 찾아서 푼 문제라 엄청 뿌듯하기도 하고, 점화식을 찾는데도 시간이 꽤 걸렸지만 너무나도 행복하다 ㅎㅎ solved.ac 이용해서 난이도 확인해 봤는데 실버1이라니.. ㅎ 근데 시간을 더 올리는게 중요하겠음. 어떻게 풀었냐면 아래 사진을 참고하면 좋을듯하다. 🟠 예전에 어떤 글을 보다가 알고리즘 잘하는 사람은 손으로 안하고 머리로만 딱 해서 하는게 진짜 잘하는 사람이라는 글을 봤었는데, 그래서 일부러 종이를 안쓰고 머리속으로 생각하는 연습을 함. 근데 나는 아직 그정도가 아니라서 종이를 쓰면서 하는게 더 낫겠음. 🟠 dp값을 지정할 때, 나는 주로 dp[1]과 dp[2]를 먼저 세팅해주는데, 문제..

BOJ 11053 가장 긴 증가하는 부분 수열 ✅ dp라는데 진짜 어려웠다. 우선 알고리즘 풀이법이 이해가 가지 않았다. 주어진 값이 10 20 10 30 20 50 있다고 가정하자. list 10 20 10 30 20 50 dp 1 2 1 3 2 4 코드를 보면 이해할 수 있는데, 어떤 수를 기준으로 나보다 작은 수를 비교한다. 나를 기준으로 내 앞을 비교한다. 나보다 작은 수(j)라고 하면 dp[j]는 dp[j]보다 작은 값들이 몇개 있는지 저장한다. 그게 가장 긴 부분 수열의 합이기 때문이다. 제일 중요한 것은 실제 문제 풀이에서 이를 떠올려야 한다는 점이다. 그렇다면 점화식을 어떻게 생각할 수 있을까?dp문제의 경우에는 그냥 손으로 쓰다보면 특정한 패턴을 찾을 수 있다.list를 놓고, 나보다 작..

BOJ 2579 계단 오르기 ✅ 점화식을 이용한 DP문제였다. 나동빈 책을 공부하면서 비슷한 문제를 해결하려는 노력을 했었는데, 진짜 너무나도 어려웠다. 여기서는 점화식을 세우기 위해 문제의 마지막 조건의 초점을 맞추는데, 마지막 계단은 꼭 밟아야 한다. 이 문장을 기준으로 점화식을 설계해보자!!!! 마지막 계단을 꼭 밟아야 하므로, 마지막 계단을 밟는 케이스를 보자면1. O X O O (끝 계단과 바로 이전 계단을 밟음, 3연속은 안된다, 근데 최댓값을 찾아야 하므로 전전전칸도 포함한다.)2. ? O X O(끝 계단과 그 전전 계단을 밟음) 케이스 1에서는 끝 패턴이 저걸로 고정 케이스 2에서는 끝 패턴이 저렇게 고정 ? 자리는 어떤게 올지 모른다는 말 -> 따라서 수식에 반영하지 않는다. 이를 점화식..

프로그래머스 LV2. 땅따먹기 ✅ 프로그래머스 LV2. 땅따먹기를 푸는데 생각보다 많이 어려웠음. 처음에는 최댓값 찾고 다음 Index의 값을 0으로 세팅하려고 했는데, 그러니까 실패함 -> 잘못된 접근 그래서 다음으로는 점화식을 찾아보려고 했는데, 에러 케이스를 스스로 발견하고 다른 방법을 고민함. 구글링 결과 어떤 분에게서 아이디어를 얻었는데, 이번에 느낀 점은 이러한 풀이 방식도 있다는 것을 기억하고, 문제 접근하는데 더 열린 사고로 다가가야겠음. 사실 그냥 여러 케이스를 경험해 보면서, 어떠한 문제를 만났을 때 이전에 시도해 본 방법 중 하나가 기억에 떠올라 그 방법을 풀기를 기대하는 측면이 더 큼. 일단 처음에는 정답은 맞았으나, 효율성을 0점을 받았는데, max의 parameter로 3개의 값..

프로그래머스 LV2. JadenCase 문자열 만들기 ✅ 프로그래머스 LV2. JadenCase 문자열 만들기 이거 왜 포스팅 하냐면, 코딩 테스트에서 dumped core 나는 경우 먼저 확인해 보고자 하는 의미에서 포스팅함. 물론 알고리즘이 정확하다고 가정 아래 코드에서 7번 줄의 주석을 보면 코드를 수정한 것을 볼 수 있는데, 주석 처럼 작성하니 에러가 났음 func solution(_ s:String) -> String { let s = s.components(separatedBy: " ").map { $0.lowercased() } var answer = [String]() s.forEach { str in if ((str.first?.isLetter) != nil) { // str.first!..

프로그래머스 LV2. 모음사전 ✅ 이 문제를 푸는데 고등학교 시절에 확률과 통계 배웠던 기억이 팍팍 났음. 근데 뭔가 바로 안풀렸는데, 이걸 또 종이에 손으로 하다 보니까 패턴을 금방 발견할 수 있었음. 🟠 패턴 1. A 2. AA 3. AAA 4. AAAA 5. AAAAA 6. AAAAE 7. AAAAI 8. AAAAO 9. AAAAU 10. AAAE _ _ _ _ _ 이렇게 다섯자리가 있다고 가정하면 맨 끝자리의 변화는 1씩 카운트 된다. 그렇다면 4번째 자리는 어떻게 일반화 할까? 5번째 자리에 올 수 있는 경우의 수가 5가지이므로 거기에 +1을 하면 된다. 따라서 문자의 index * 6이다. 그럼 3번째 자리는? 4,5 번 자리에 각각 5, 5개씩 올 수 있으므로 25개, 4번자리를 스킵하고 5..

프로그래머스 LV2. 튜플 ✅ 문제를 이해하기가 어려웠지 푸는데 어렵지는 않았음. 근데 왜 포스팅하냐면, 푸는데 오래걸려서. 정규 표현식으로 분리하려고 했는데, 사용하기가 불편했고, split을 통해서 "}"로 분리해서 작업을 했더니, 원하는 형태로 바꾸는데 for이 많이 들어가서 코드가 별로가 되었음. 근데 코드를 보니까 분리를 "},{"로 가능해 보여서 그렇게 설계함. 문제를 풀고난 후에 구글링을 하면서 코드 리팩토링까지 마침. component와 split에 대해서 더 자세히 알아야겠다고 다짐하며 마침. 🟠 문제에서 이해가 가지 않는 부분 해석 "{{4,2,3},{3},{2,3,4,1},{2,3}}" // [3, 2, 4, 1] {3} {2,3} {4,2,3} {2,3,4,1} 이렇게 순서로 봐야한..

프로그래머스 LV. 2 N개의 최소공배수 ✅ 최소공배수와 최대공약수를 사용할 때는 직접 구하지 말고 유클리드 호제법을 이용하자. 호제법을 이용한다면 쉽게 풀수가 있다. struct p12953 { static func run() { print(p12953.solution([2,6,8,14])) // 168 } static func solution(_ arr:[Int]) -> Int { // 최소공배수 찾는 알고리즘 하나 마련해서 쭉 돌자 var prev = arr[0] for i in 1.. Int { return (a * b) / gcd(a, b) } // 최대공약수 static func gcd(_ a: Int, _ b: Int) -> Int { var a = a var b = b var r = 0 w..

프로그래머스 LV2. 삼각 달팽이 ✅ 프로그래머스 LV2. 삼각 달팽이 아주 오래걸린 문제였다. 여러가지 방법이 있었는데, 처음에는 배열을 [ [], [], [], [] ] 이런 식으로 세팅해 두어서 insert와 append로 알고리즘을 작성하니까 너무나도 어려웠다. 근데 그냥 n = 3이라고 가정하면, [ [0,0,0], [0,0,0], [0,0,0] ] 이렇게 세팅하고 푸니까 우선 훨씬 쉬워질 수 있었다. 왜냐하면 index를 [row][col]로 접근할 수 있어서!! 문법적으로는 2가지를 보면 된다. 1. 2차원 배열을 크기를 주어서 만드는 방법과 2. flatMap을 사용한 부분 🟠 알고리즘을 떠올리는 과정 이걸 곰곰이 생각해보니까, [ 1 ] [ 2, 9 ] [ 3 ,10 ,8 ] [ 4, 5..

프로그래머스 LV2. 피로도 ✅ 프로그래머스 LV2. 피로도 나 이제 재귀를 조금 잘쓰는 것 같다. 물론 완전 탐색에서의 재귀이지만, dfs, bfs 등도 잘 풀 수 있어야 하니 꾸준히 노력하자 갑자기 적는거지만 알고리즘 왜 푸냐면 개인적으로 앱 개발에 있어서 어떠한 알고리즘이라 로직 처리를 할 때 매우 약하다. 그런 점을 보완하고자 알고리즘을 공부한다. import Foundation struct p87946 { static func run() { print(p87946.solution(80, [[80,20],[50,40],[30,10]])) // 3 } static var count = 0 static var results: Set = [] static func solution(_ k:Int, _ d..