신경망 학습에서 초기 가중치 설정
신경망 학습에서 특히 중요한 것이 가중치의 초깃값 설정은 중요함.
특히, 가중치의 초기값을 무엇으로 설정하는지에 따라서 신경망 학습의 성패가 달라질 수 있음.
목차
- 초깃값을 0으로 설정
- 은닉층의 활성화 값 분포
- Xavier 초깃값
- 시각화 코드 샘플
초깃값을 0으로 설정
오버피팅을 억제해 범용 성능을 높이는 테크닉인 가중치 감소(weight decay) 기법을 소개하고자 함.
가중치 감소는 가중치 매개변수의 값이 작아지도록 학습하는 방법으로 가중치의 값을 작게하여 오버피팅이 일어나지 않게 하는 것.
하지만, 가중치를 0으로 설정하면 학습이 올바로 이뤄지지 않음.
왜냐하면 오차역전파법에서 모든 가중치의 값이 똑같이 갱신되기 때문.
가중치들은 같은 초깃값에서 시작하고, 갱신을 거쳐도 여전히 같은 값을 유지.
이는 결국 가중치를 여러개 같는 의미가 사라지게 되며, 가중치가 고르게 되어 버리는 상황을 막으려면 초깃값을 무작위로 설정해야 함.
은닉층의 활성화 값 분포
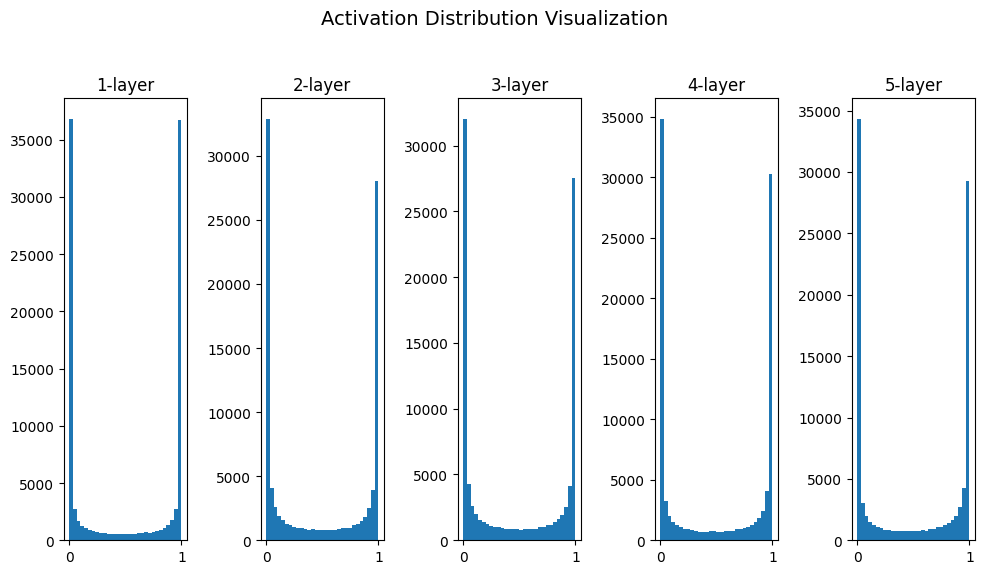
표준편차가 1인 정규분포
- 활성화 값이 0과 1에 주로 분포되어 미분값이 0에 가까워 지도록 하여서 결국 역전파의 기울기 값은 점점 작아지다가 사라지는 기울기 소실 문제가 발생하여, 층이 깊어질수록 기울기가 더 사라지게 됨.
- 즉, 기울기를 깊게하는 이유가 무색해짐
- 즉, 기울기 소실이란 부분에서 문제가 되어 딥러닝에서 심각한 문제가 발생할 수 있음.
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# --- [시뮬레이션 코드 시작] ---
x = np.random.randn(1000, 100) # 1000개의 데이터
node_num = 100 # 각 은닉층의 노드 수
hidden_layer_size = 5 # 은닉층이 5개
activations = {} # 활성화값을 저장할 빈 딕셔너리
# 데이터를 생성하고 activations 딕셔너리에 채워넣는 루프
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# 가중치 초기화 (예시로 표준편차 1 사용)
w = np.random.randn(node_num, node_num) * 1
a = np.dot(x, w)
z = sigmoid(a)
activations[i] = z
# --- [시뮬레이션 코드 끝, activations에 데이터가 채워짐] ---
표준편차가 0.01인 정규분포
- 기울기 소실 문제는 일어나지 않으나, 활성화 값이 치우쳐서, 표현력 관점에서는 큰 문제가 발생함.
- 즉, 이 상황에서는 다수의 뉴런이 거의 같은 값을 출력하고 있어서 여러개의 뉴런이 있는게 무색해짐.
- 즉, 표현력을 제한한다는 관점에서 문제가 됨

def sigmoid(x):
return 1 / (1 + np.exp(-x))
# --- [시뮬레이션 코드 시작] ---
x = np.random.randn(1000, 100) # 1000개의 데이터
node_num = 100 # 각 은닉층의 노드 수
hidden_layer_size = 5 # 은닉층이 5개
activations = {} # 활성화값을 저장할 빈 딕셔너리
# 데이터를 생성하고 activations 딕셔너리에 채워넣는 루프
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# 가중치 초기화 (예시로 표준편차 0.01 사용)
w = np.random.randn(node_num, node_num) * 0.01
a = np.dot(x, w)
z = sigmoid(a)
activations[i] = z
# --- [시뮬레이션 코드 끝, activations에 데이터가 채워짐] ---
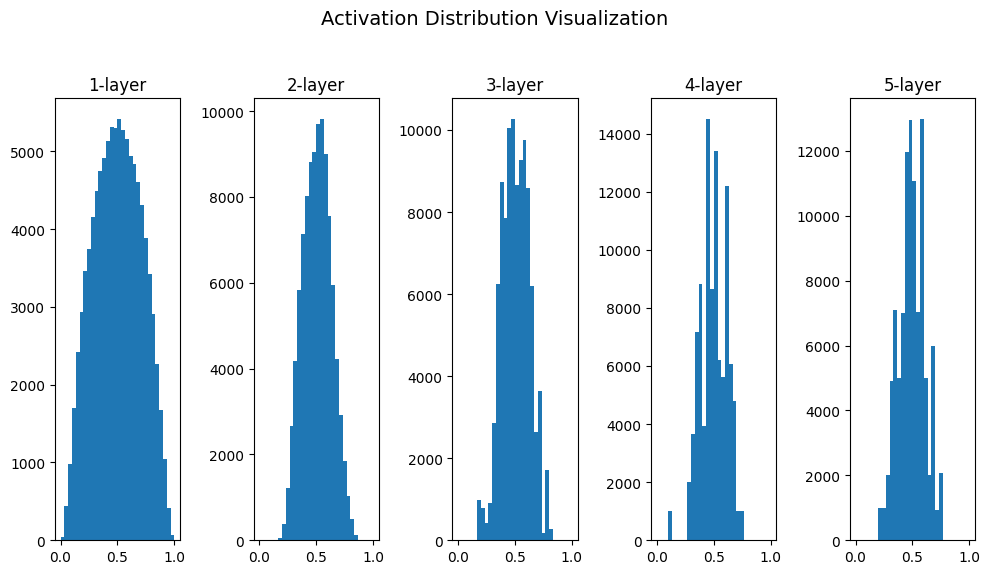
Xavier 초깃값
활성화 값은 적당히 고루 분포되어야 함.
다양한 데이터가 흐르게 해야 학습이 효율적이기 때문
앞 계층의 노드가 n개라면 표준편차가 (1/루트 n)인 분포를 사용.
Xavier 초기값을 이용하면 앞 층의 노드가 많을수록 대상 노드의 초깃값으로 설정하는 가중치가 좁게 퍼짐.
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# --- [시뮬레이션 코드 시작] ---
x = np.random.randn(1000, 100) # 1000개의 데이터
node_num = 100 # 각 은닉층의 노드 수
hidden_layer_size = 5 # 은닉층이 5개
activations = {} # 활성화값을 저장할 빈 딕셔너리
# 데이터를 생성하고 activations 딕셔너리에 채워넣는 루프
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# 가중치 초기화 (예시로 표준편차 1 사용)
w = np.random.randn(node_num, node_num) / np.sqrt(node_num)
a = np.dot(x, w)
z = sigmoid(a)
activations[i] = z
# --- [시뮬레이션 코드 끝, activations에 데이터가 채워짐] ---
He 초깃값
Xavier 초깃값은 활성화 함수가 선형인 것을 전제로 이끈 결과
sigmoid 함수와 tanh 함수는 대칭이라 중앙 부근이 선형인 함수로 볼 수 있음. 그래서 Xavier 초깃값이 적당.
하지만, ReLU를 이용할 때는 ReLU에 특화된 초깃값을 이용하라고 권장.
이때 He 초깃값을 사용함.
시각화 코드 샘플
1. 은닉층의 활성화 값 분포
# --- [시각화 코드 시작] ---
plt.figure(figsize=(10, 6))
# 이제 activations 딕셔너리에 데이터가 있으므로 루프가 실행됩니다.
for i, a in activations.items():
plt.subplot(1, hidden_layer_size, i+1)
plt.title(str(i+1) + "-layer")
# 수정 필요: a.flatten()은 함수 호출이므로 괄호를 추가해야 합니다.
# 또한, hist 함수의 bins와 range 인자명을 명시적으로 적는 것이 좋습니다.
plt.hist(a.flatten(), bins=30, range=(0,1))
plt.suptitle('Activation Distribution Visualization', fontsize=14)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()
# --- [시각화 코드 끝] ---
'AI > DeepLearning' 카테고리의 다른 글
| 오버피팅, 가중치 감소, 드롭아웃 (0) | 2025.11.14 |
|---|---|
| 배치 정규화 Batch Normalization + Pytorch 실습 (0) | 2025.11.13 |
| SGD, Momentum, AdaGrad, RMSprop, Adam (0) | 2025.11.09 |
| 활성화 함수 계층 기본 구현 정리 (0) | 2025.11.09 |
| 경사하강법 (Gradient Descent) (1) | 2025.11.09 |