활성화 함수 계층 기본 구현 정리
신경망을 구성하는 층을 각각에 대해서 기본적인 것들을 정리.
아래 샘플 코드에서 사용되는 주요 Numpy와 Python 문법 정리
이거 모르면 아래 코드 읽는데 상당히 어려움.
주로 사용하는 언어가 정적 타이핑언어인데, 동적 타이핑 언어를 사용하는 경우 사고 전환이 아직까지도 좀 불편한 부분이 있어서 차이점을 느끼는 부분을 위주로 정리하고자 함.
1. 파이썬에서는 인스턴스 변수는 __init__에서 선언하는 것이 원칙.
하지만 새롭게 만든다고해서 동작하지 않는것은 아님.
class SomeClass:
def __init(self):
self.mask = None
2. numpy에서 불리언 인덱싱 문법
True/False 배열을 이용해서 원하는 위치만 선택하는 기법
mask를 출력해보면 x와 동일한 형상의 배열로 결과를 반환함.
import numpy as np
x = np.array([1, -2, 3, -4, 5])
mask = x <= 0 # x가 0 이하인 위치를 True로 표시
print(mask) # [False True False True False]
선택된 원소만 변경하려면 아래처럼 코드를 작성함.
import numpy as np
x = np.array([1, -2, 3, -4, 5])
mask = (x <= 0)
x[mask] = 0 # mask가 True인 위치의 원소를 0으로 바꿔라
print(x) # [1 0 3 0 5]
3. np.exp()는 numpy의 지수함수
시그모이드 함수를 구현할 때 참고
np.exp(a) # e에 a제곱 (e는 자연상수)
ReLU 계층
ReLU에서는 0이상의 값만 활성화하므로 이게 맞춰서 구현
- 순전파 구현
- 값이 0보다 작으면 0으로 만들고 그보다 크면 그대로 흘려 보낸다.
- 역전파 구현
- 값이 0이면 이미 죽은 노드라서 0처리하고 0보다 크면 기울기를 그대로 전달한다.

class Relu:
def __init(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dout
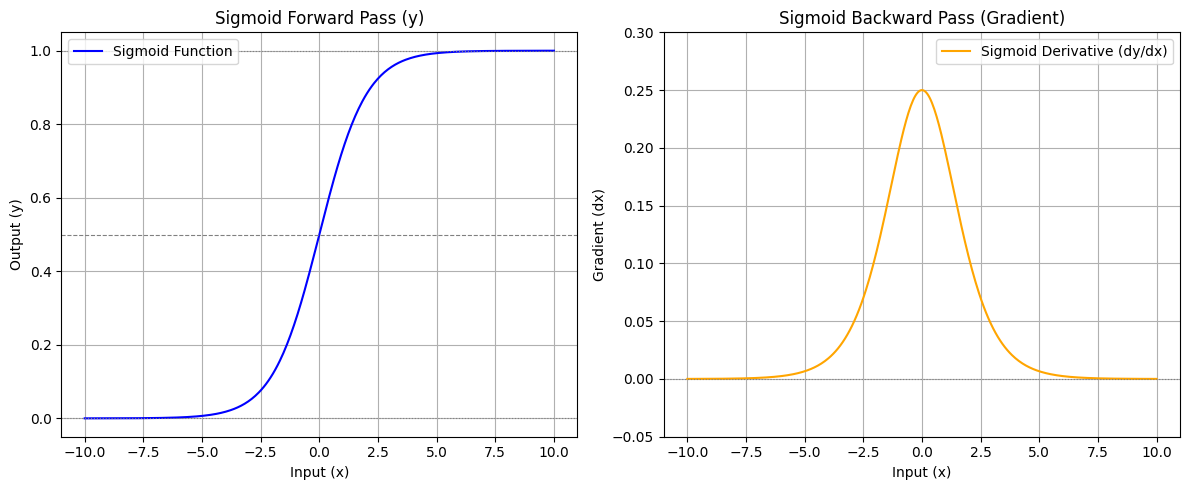
Singmoid 계층
시그모이드 함수의 정의와 도함수 식
도함수를 구하는 과정은 손으로 직접 계산. (그렇게 어렵지 않음)


시그모이드 함수의 그래프
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
Affine 계층
행렬의 곱은 기하학에서는 어파인 변환(Affine transformation)이라고 함.
행렬의 곱 계산은 대응하는 차원의 원소의 수를 일치시키는 것이 핵심
X = np.random.rand(2) # 입력
W = np.random.rand(2, 3) # 가중치
B = np.random.rand(3) # 편향
print(X.shape) # (2,)
print(W.shape) # (2,3)
print(B.shape) # (3,)
Y = np.dot(X, W) + B
print(Y, Y.shape) # [0.70639743 0.69957377 0.99991712] (3,)
기존에는 스칼라 값이 흘렀다면, 이번부터는 노드 사이에 행렬이 흐름.
배치용 Affine 계층
데이터 N개를 묶어서 순전파하는 경우 즉, 배치용 Affine 계층을 생각.
(묶은 데이터를 배치라고 부름)
X_dot_W = np.array([[0,0,0], [10,10,10]])
B = np.array([1,2,3])
X_dot_W + B
# X_dot_W의 출력
[[ 0 0 0]
[10 10 10]]
# X_dot_W + B의 출력
array([[ 1, 2, 3],
[11, 12, 13]])
Affine의 구현
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dxSoftmax-with-Loss 계층
출력층에서 사용하는 소프트맥스 함수
입력 값을 정규화하여 출력.
신경망에서 수행하는 작업은 학습과 추론.
추론할 때는 일반적으로 Sotfmax 계층을 사용하지 않음.
마지막 Affine 계층의 출력을 인식 결과로 이용.
신경망에서 정규화하지 않는 출력 결과 (Softmax 앞의 Affine 계층의 출력)를 점수(Score)라고 합니다.
신경망 추론에서 답을 하나만 내는 경우에는 가장 높은 점수만 알면 되니 Softmax 계층은 필요 없지만, 신경망을 학습할 때는 Softmax 계층이 필요.
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 손실
self.y = None # softmax의 출력
self.t = None # 정답 레이블(원-핫 벡터)
def forward(self, x, t):
self.t = t
self.y = softmax(x) # 3.5.2, 4.2.2에서 구현
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = self.y - self.t / batch_size
return dx
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # 오버플로 대책
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
'AI > DeepLearning' 카테고리의 다른 글
| 신경망 학습에서 초기 가중치 설정 (0) | 2025.11.13 |
|---|---|
| SGD, Momentum, AdaGrad, RMSprop, Adam (0) | 2025.11.09 |
| 경사하강법 (Gradient Descent) (1) | 2025.11.09 |
| 오차역전파 (0) | 2025.11.05 |
| 신경망 학습 (Neural Network Training) (0) | 2024.04.23 |