Dijkstra 알고리즘
✅ Dijkstra 알고리즘을 구현해보자.
이번 포스팅에서는 스위프트 데이터 구조와 알고리즘 책과 나동빈 파이썬 알고리즘 책 그리고 다른 분의 포스팅을 참고하여 작성하였음.
이거 예전에 손을 풀때는 참 이해도 쉽고 그랬는데, 알고리즘 공부 놓고 다시 시작하려니까 어려웠음. 근데 그냥 상당히 집중이 안되는 시기인 것 같다.
아래의 그래프를 다익스트라 알고리즘을 손으로 분석해보자.
나동빈 책에 따르면 다익스트라 알고리즘과 플로이드 워셜 알고리즘을 소개해주는데 둘의 차이를 분석해보자.
다익스트라 알고리즘 : 한 지점에서 각각의 특정 지점까지의 최단 경로 - 그리디에 속함
플로이드 워셜 알고리즘 : 모든 지점에서 다른 모든 지점까지의 최단 경로 - dp에 속함
간선의 개수 : E
노드의 개수 : V
시간복잡도는 O(ElogV)
✅ 다익스트라 알고리즘
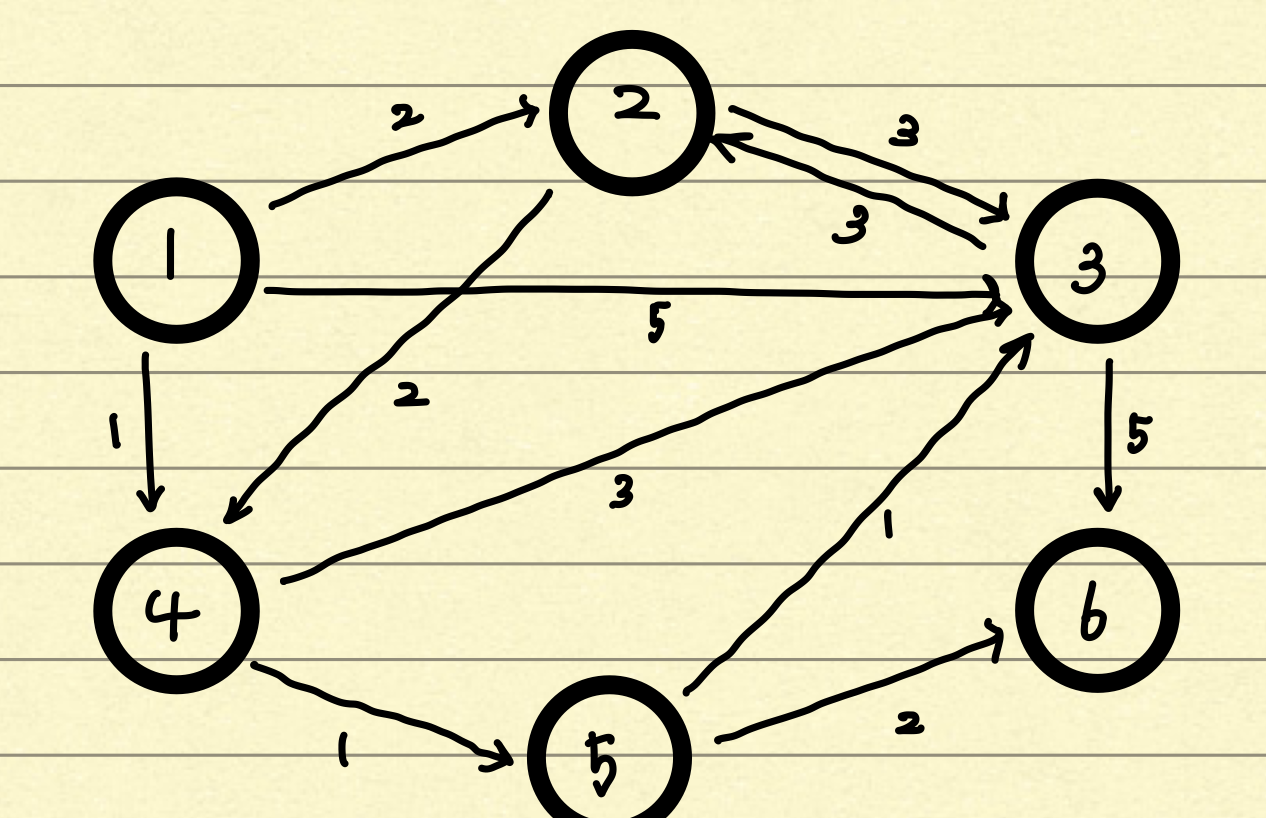
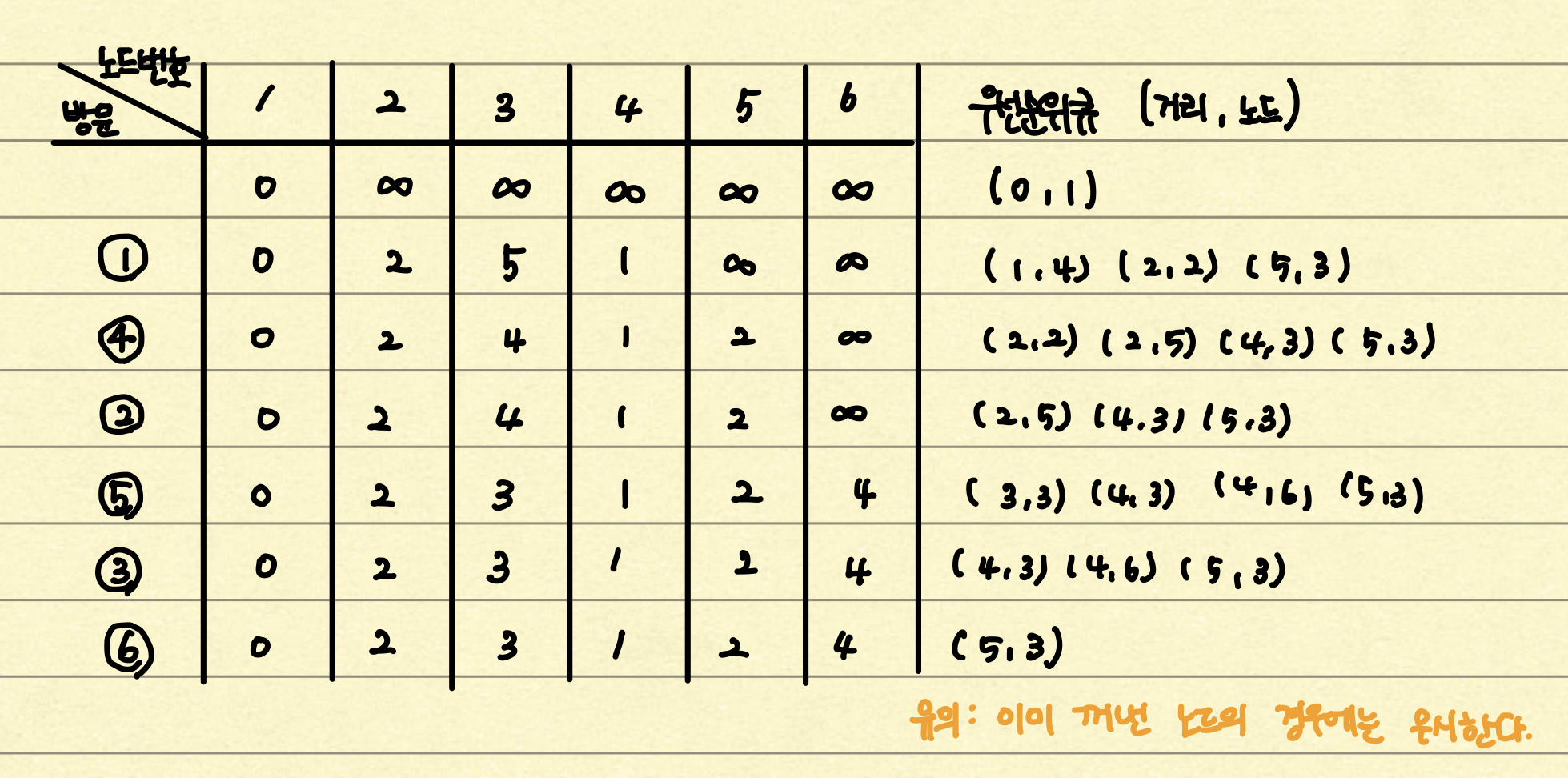
✅ 코드
struct NodePriority: Comparable {
static func < (lhs: NodePriority, rhs: NodePriority) -> Bool {
lhs.priority > rhs.priority
}
var node: String = ""
var priority: Int = 0
}
func dijkstra(graph: [String: [String: Int]], start: String) -> [String: Int] {
var distances: [String: Int] = [:]
var priorityQueue = MaxHeap(NodePriority.init(node: start, priority: 0))
for key in graph.keys {
let value = key == start ? 0 : 2147483647
distances.updateValue(value, forKey: key)
}
while !priorityQueue.isEmpty {
guard let popped = priorityQueue.pop() else { break }
if distances[popped.node]! < popped.priority {
continue
}
for (node, priority) in graph[popped.node]! {
let distance = priority + popped.priority
if distance < distances[node]! {
distances[node] = distance
priorityQueue.insert(NodePriority.init(node: node, priority: distance))
}
}
}
return distances
}
let graph: [String: [String: Int]] = [
"A" : ["B": 9, "C" : 1, "D" : 15],
"B" : ["E": 10],
"C" : ["B": 5, "E" : 3],
"D" : ["E": 10],
"E" : ["F": 7],
"F" : [:]
]
힙에 대한 코드는 아래 포스팅에 있습니다.
2022.04.08 - [코딩테스트/자료구조 및 알고리즘] - [Swift] Heap에 대해서 알아보자
(참고)
https://babbab2.tistory.com/110?category=908012
Swift) 최단 경로 :: 다익스트라(Dijkstra) 구현 해보기
안녕하세요:) 소들입니다! 이번 포스팅은 최단 경로 알고리즘 중 하나인, 다익스트라에 대해 공부해볼 거예요!!!!! 조금 어려울 수 있지만!!!! 내가보기엔 이론보다 이름이 젤 어려운듯; 먼저, 최
babbab2.tistory.com
'Archive > 자료구조와 알고리즘' 카테고리의 다른 글
| [Swift] 크루스칼 알고리즘과 위상정렬 (0) | 2022.05.15 |
|---|---|
| [Swift] 플로이드 워셜 알고리즘 (0) | 2022.04.10 |
| [이것이 코딩 테스트다] chapter 5. DFS/BFS (0) | 2022.04.01 |
| [이것이 코딩 테스트다] chapter 8. DP (0) | 2022.04.01 |
| Swift Data Structure and Algorithms (0) | 2021.10.28 |